Goodman-Bacon分解

# install.packages(c("ggplot2", "fixest", "bacondecomp"))
library(ggplot2)
library(fixest)
library(bacondecomp)

# 可选：自定义ggplot2主题
theme_set(
    theme_linedraw() +
    theme(
        panel.grid.minor = element_line(linetype = 3, linewidth = 0.1),
        panel.grid.major = element_line(linetype = 3, linewidth = 0.1)
    )
)

什么是Goodman-Bacon分解？

正如TWFE部分末尾所讨论的，引入差异处理时机使得很难在处理前和处理后时期之间划清界限。让我们继续使用该部分最后一个示例中使用的相同数据集。

dat4 = data.frame(
    id = rep(1:3, times = 10),
    tt = rep(1:10, each = 3)
    ) |>
    within({
        D = (id == 2 & tt >= 5) | (id == 3 & tt >= 8)
        btrue = ifelse(D & id == 3, 4, ifelse(D & id == 2, 2, 0))
        y = id + 1 * tt + btrue * D
    })

以图形形式：

ggplot(dat4, aes(x = tt, y = y, col = factor(id))) +
    geom_point() + geom_line() +
    geom_vline(xintercept = c(4.5, 7.5), lty = 2) +
    scale_x_continuous(breaks = scales::pretty_breaks()) +
    labs(x = "时间变量", y = "结果变量", col = "ID")

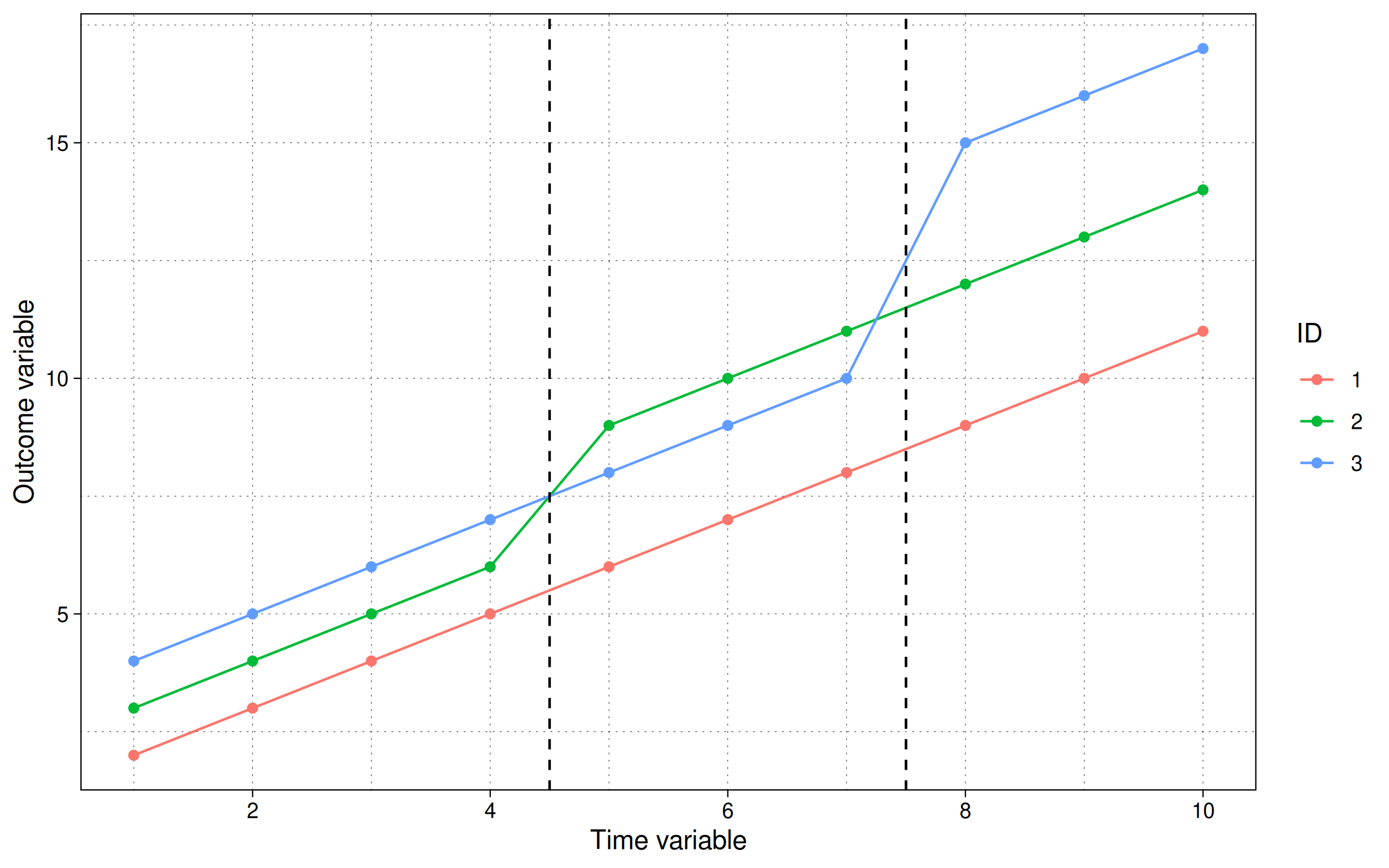
这里我们看到我们的模拟包括两个不同的处理时期。第一个处理发生在第5期，其中id=2的趋势线增加了2个单位。第二个处理发生在第8期，其中id=3的趋势线增加了4个单位。相比之下，id=1在整个实验期间保持未处理状态。

回过头来，如何计算ATT并不立即清楚。例如，后期处理单元（id=3）应该如何看待早期处理单元（id=2）？后者能否用作前者的对照组？毕竟，它们没有同时接受处理…但是，另一方面，id=2的路径已经被初始处理波改变。

为了解开这个难题，让我们先估计一个简单的TWFE模型。

feols(y ~ D | id + tt, dat4)

OLS估计，因变量：y
观察值：30 
固定效应：id：3，tt：10
标准误差：按id聚类 
      估计量 标准误差 t值 Pr(>|t|)    
DTRUE  2.90909   0.725719 4.00856 0.056967 .  
---
显著性代码： 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
RMSE: 0.35505     调整R2: 0.986455
                组内R2: 0.831169

结果系数估计\(hat{\beta}=2.91\)代表什么？简短的答案是它包括一个加权平均的四个不同2×2组（或比较）：

处理与未处理 1) 早期处理(\(T^e\))与未处理(\(U\)) 2) 晚期处理(\(T^l\))与未处理(\(U\))
差异处理 1) 早期处理(\(T^e\))与晚期对照(\(C^l\)) 2) 晚期处理(\(T^l\))与早期对照(\(C^e\))

我们可以如下可视化这四个比较集：

rbind(
    dat4 |> subset(id %in% c(1,2)) |> transform(role = ifelse(id==2, "处理", "对照"), comp = "1.1. 早期与未处理"),
    dat4 |> subset(id %in% c(1,3)) |> transform(role = ifelse(id==3, "处理", "对照"), comp = "1.2. 晚期与未处理"),
    dat4 |> subset(id %in% c(2,3) & tt<8) |> transform(role = ifelse(id==2, "处理", "对照"), comp = "2.1. 早期与未处理"),
    dat4 |> subset(id %in% c(2:3) & tt>4) |> transform(role = ifelse(id==3, "处理", "对照"), comp = "2.2. 晚期与未处理")
) |>
    ggplot(aes(tt, y, group = id, col = factor(id), lty = role)) +
    geom_point() + geom_line() + 
    facet_wrap(~comp) +
    scale_x_continuous(breaks = scales::pretty_breaks()) +
    scale_linetype_manual(values = c("对照" = 5, "处理" = 1)) +
    labs(x = "时间变量", y = "结果变量", col = "ID", lty = "角色")

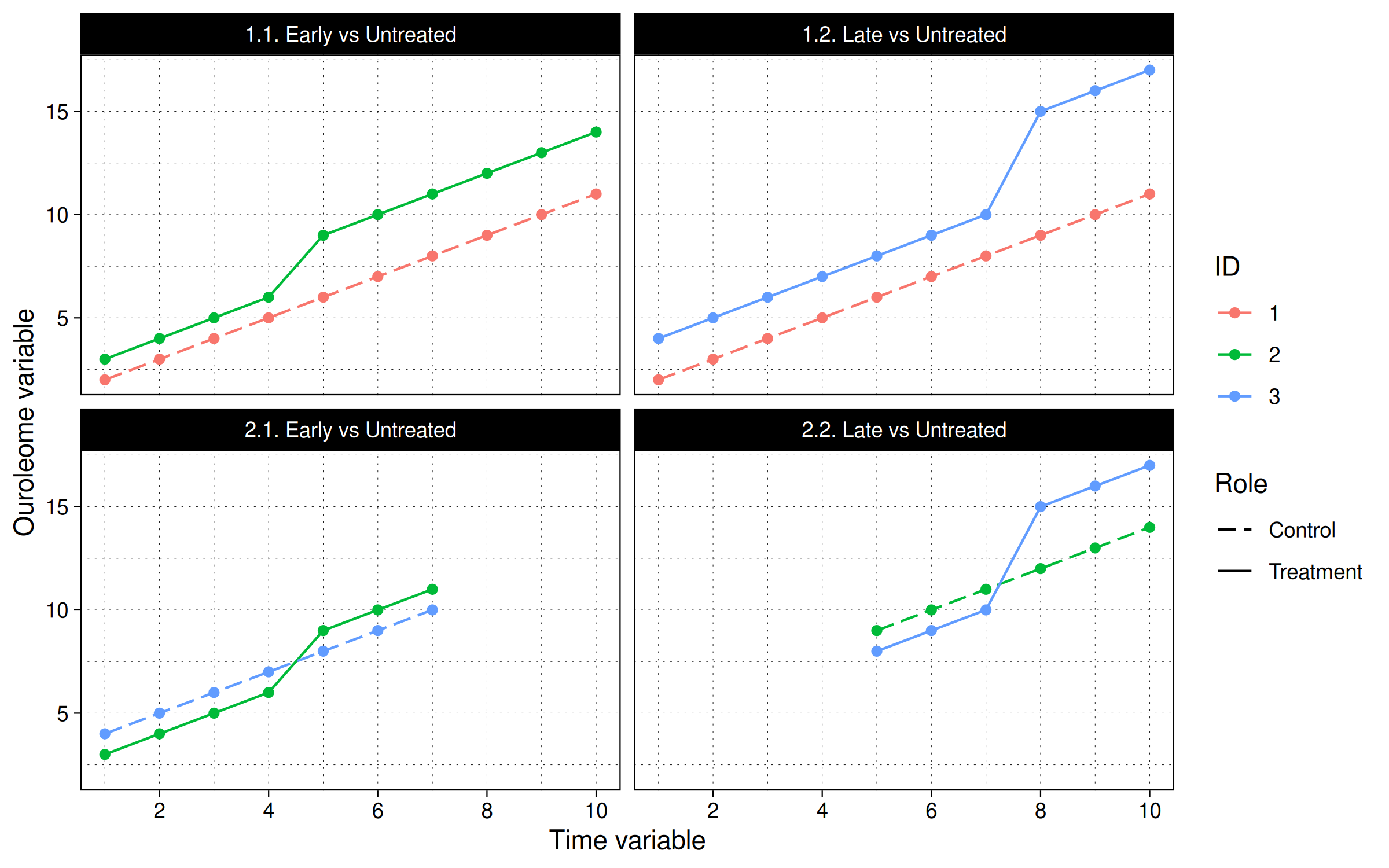
换句话说，面板ID根据首次处理发生的时间以及它与其他面板ID的处理关系被分成不同的时机队列。面板ID越多，处理时机差异越大，上述组合就越多。

Goodman-Bacon分解隔离这些2×2比较，并根据它们在数据中的相对覆盖范围（即，每个比较相对于整体时间跨度持续多长时间，以及涉及多少单元）为它们分配权重。

要在R中实现Goodman-Bacon分解，我们只需要调用bacondecomp包中的bacon()函数。包的简介可在这里获得，尽管参数非常不言自明。让我们看看它对我们当前问题产生什么结果：

(bgd = bacon(y ~ D, dat4, id_var = "id", time_var = "tt"))

  处理 未处理 估计量    权重                     类型
     5       Inf        2 0.3636364     处理与未处理
     8       Inf        4 0.3181818     处理与未处理
     8         5        4 0.1363636 晚期与早期处理
     5         8        2 0.1818182 早期与晚期处理

这里我们得到了我们的权重和每个组的2×2\(\beta\)。该表告诉我们(\(T\) vs \(U\))，这是晚期和早期处理与从未处理的总和，具有最大的权重，其次是早期与晚期处理，最后是晚期与早期处理。

重要的是，注意这些估计量的加权均值与我们早期的（朴素）TWFE系数估计完全相同。再次强调，这不应该令人惊讶，因为整个Bacon-Goodman练习的重点是分解该估计量的构成，从而突出潜在的偏差来源。

(bgd_wm = weighted.mean(bgd$estimate, bgd$weight))

[1] 2.909091

我们可以轻松地绘制这个结果来可视化不同分量如何影响整体估计。

ggplot(bgd, aes(x = weight, y = estimate, shape = type, col = type)) +
  geom_hline(yintercept = bgd_wm, lty  = 2) +
  geom_point(size = 3) +
  labs(
    x = "权重", y = "估计量", shape = "类型", col = "类型",
    title = "Bacon-Goodman分解示例",
    caption = "注：水平虚线表示完整TWFE估计量。"
    )

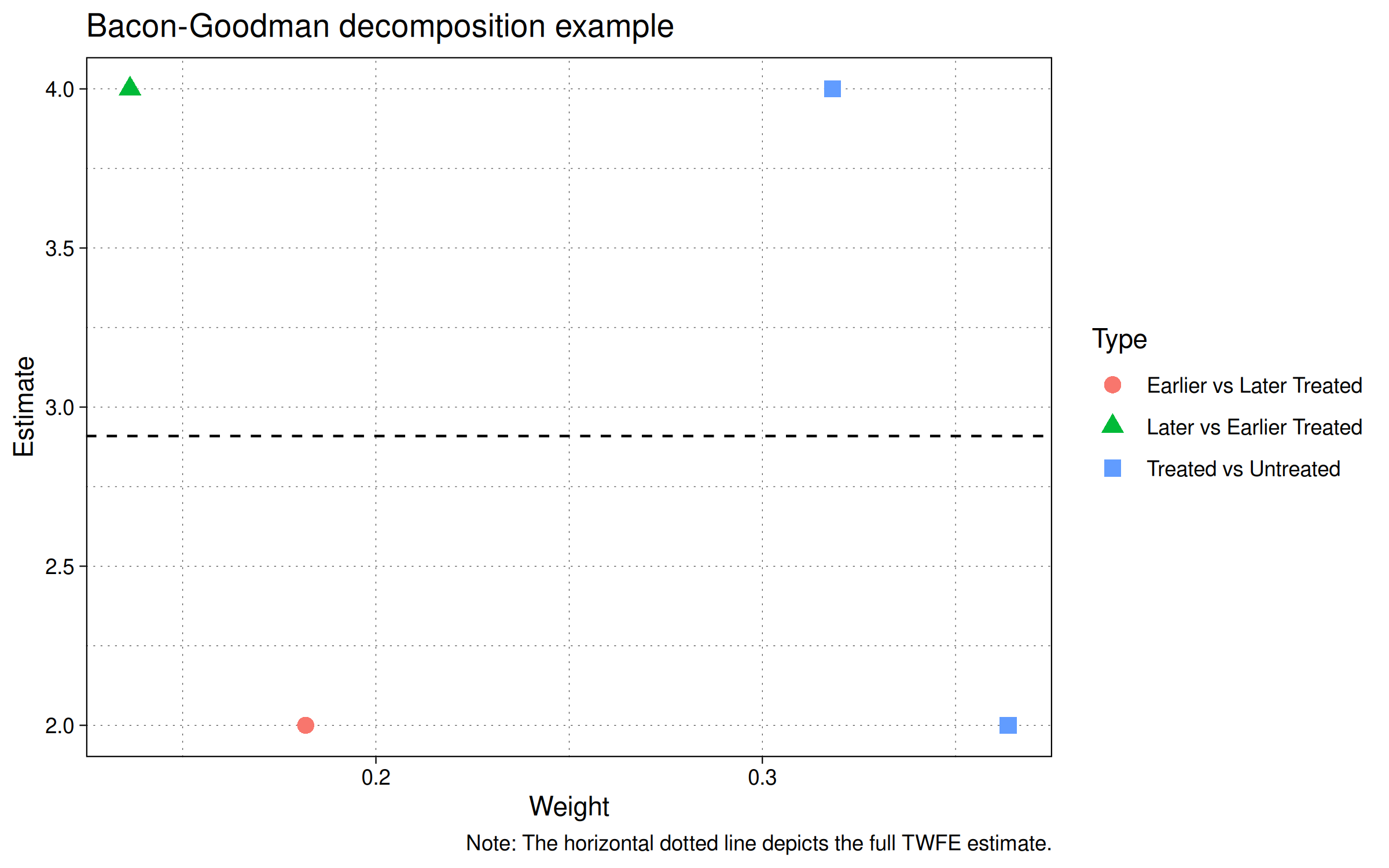
该图显示了我们示例中四个组的四个点。

早期与晚期处理（红色圆圈）。
晚期与早期处理（绿色三角形）。
处理与未处理（两个蓝色方块；一个用于早期处理组，另一个用于晚期处理组）。

最后，注意估计值2和4与我们模拟中编码的处理效应一致。具体来说，单元id=2增加2，单元id=3比未处理单元id=1增加4。

那么TWFE回归哪里出错了？

待完成

Goodman-Bacon分解

目录

什么是Goodman-Bacon分解？

那么TWFE回归哪里出错了？